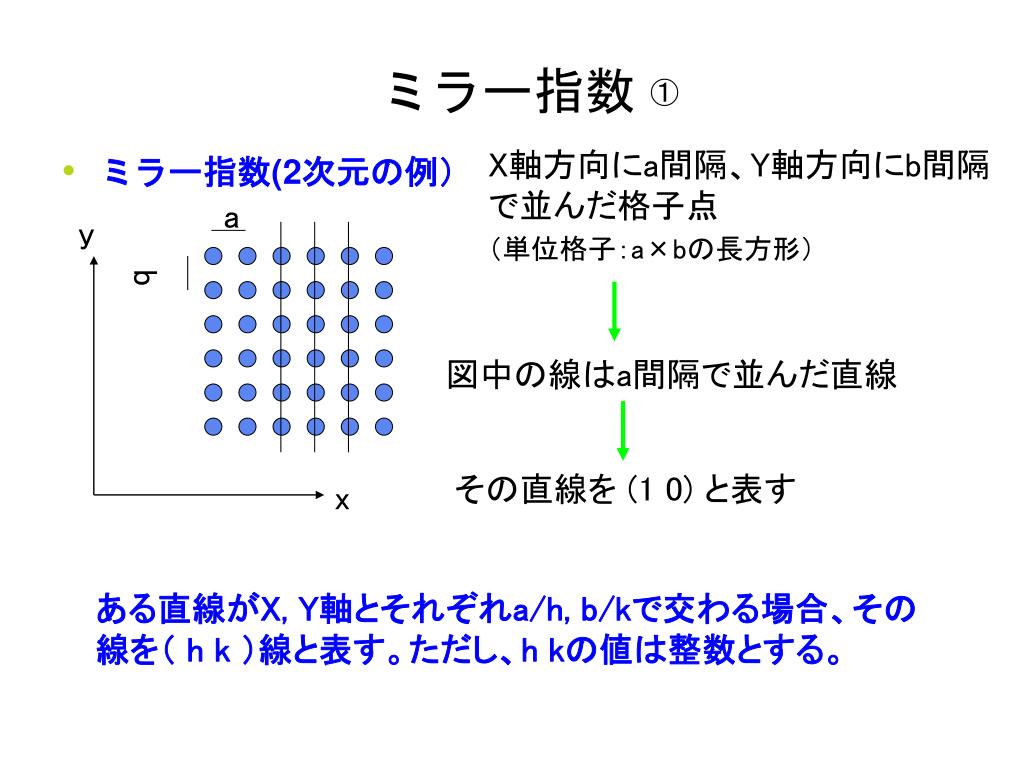
六方晶系の面指数 a b d a b c a b d c, , , , , o を用いる (h k l) → (h k j l) A B D a h a k O a j OAB = OAD OBD 1 1 1 sin1 sin60 sin60 2 2 2 a a a a a a h k h j j k q q q h k j = 0 利点:面の対称性が明らかになる (1 2 1) (1 1 1) (1 2 1 1) (1 1 2 1) この2つの面が等価であることがわかるA=0nm,b=094nm,c=075nmの斜方単位胞の(a){123}面と, (b){246}面の両間隔を計算せよ. 解法(a) (・3)式に格子定数とミラー指数を代入する. (b) {246}面のミラー指数は{123}面の2倍である.したがって 面間隔は1/nである. 答.011nm 0 0454 0 213nm 22 0Sep 09, 18 · 上の式の(hkl)は、格子面のミラー指数である。 ブラッグの反射条件は、結晶によるX線回折を考えるときに使われる。この記事では、ブラッグ条件がX線回折にどうかかわってくるかや、XRDの仕組みについて書く。 参考格子面とミラー指数の求め方
モデラ Advance Nanolabo ドキュメント
六方晶 ミラー指数求め方
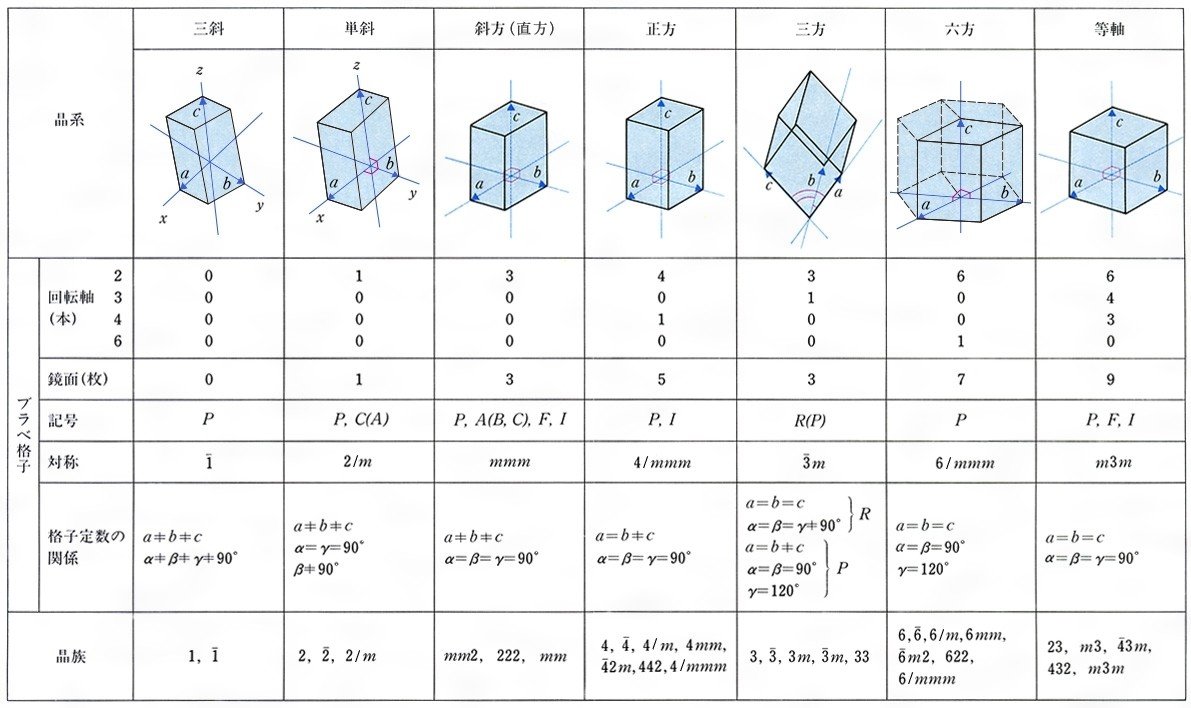
六方晶 ミラー指数求め方-斜方晶 7 ブラベー格子 正方晶 単純正方晶 体心正方晶 立方晶 単純立方晶 体心立方晶 面心立方晶 六方晶 菱面体晶 8 ブラベー格子 三斜 triclinic a b c P 単斜 monoclinic a b c = =90° P, C 斜方 orthorhombic a b c = = =90° P, I, C, F 正方 tetragonal a =b c =90° P, I 六方 hexagonal a=b cミラー指数その1:結晶における方向の記述 第7回 ミラー指数その2:六方晶におけるミラー指数 第8回 面間隔の求め方 第9回 格子欠陥(原子空孔と転位)・多結晶体 第10回 x線の発生法・特性x線について 第11回 ブラッグの条件と面の間隔 第12回



Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度
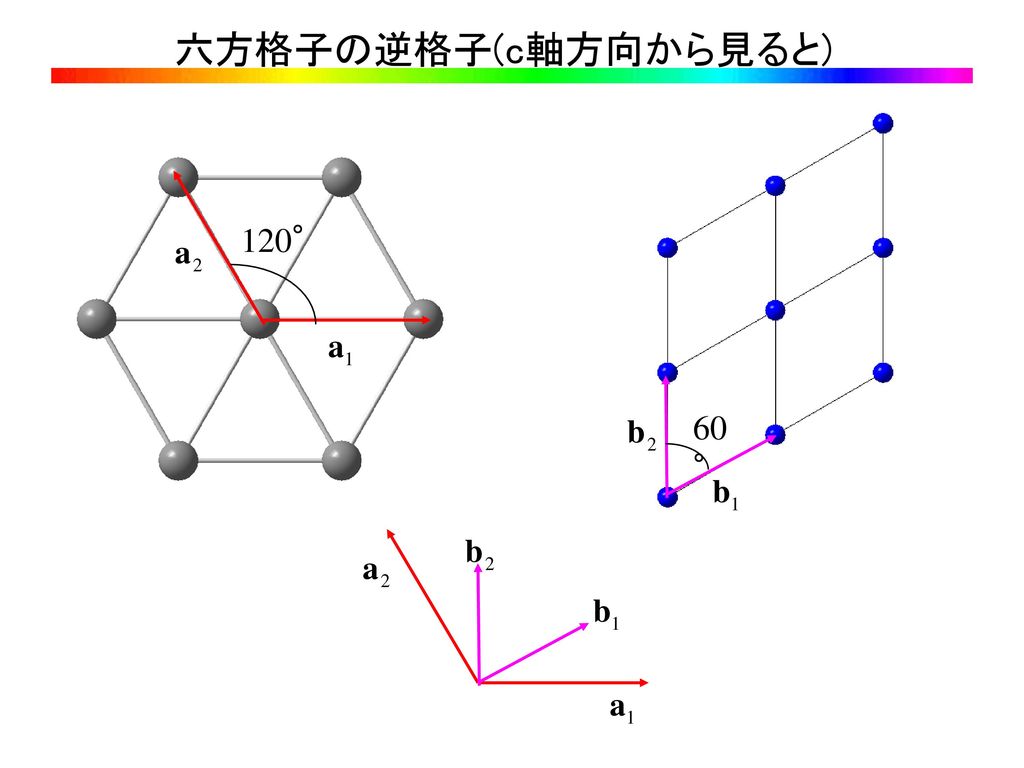
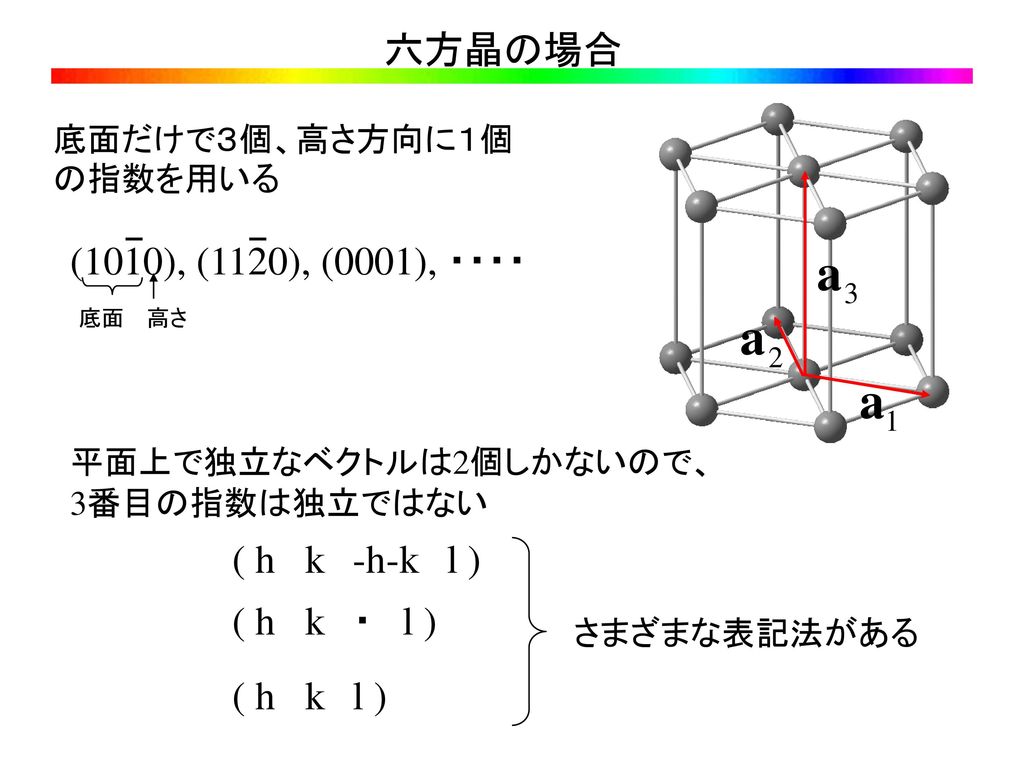
六方晶の場合 a 1 a 2 a 3 底面だけで3個、高さ方向に1個 の指数を用いる (1010), (11), (0001), ・・・・ 底面 高さ 平面上で独立なベクトルは2個しかないので、 3番目の指数は独立ではない ( hkhkl ) ( hk・l ) ( hkl ) さまざまな表記法がある反射指数 hkl から面間隔 d を求める 立方 cubic と正方 tetragonal,直方 orthorhombic 晶系の場合には,「逆単位格子の長さ」は 「格子定数の逆数」になるが,六方 hexagonal や菱面 rhombohedral,単斜 monoclinic,三かし、先に出てきた立方晶・正方晶・直方晶・六方晶については導出できるようになって おくこと。立方晶の面間隔の式くらいは憶えておこう(材料系学生には常識です)。 単斜晶 1 d2 = 1 sinβ2 (h2 a2 k2 sin2 β b2 l2 c2 − 2hlcosβ ac) 菱面体晶 1 d2 = (h2 k2 l2)sin2 α
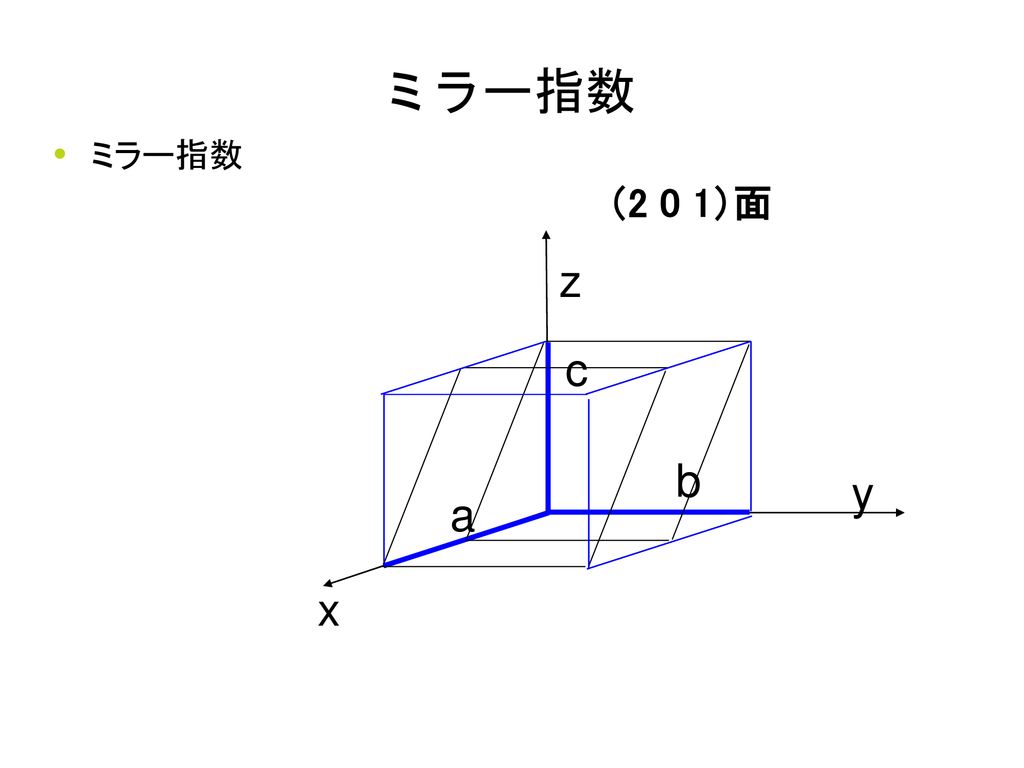
六方晶の面を表す時に ミラー指数 でお馴染みの (hklm)について どうもh k = iという関係が成り立つみたいです ;図3 ミラー指数 単位格子の外形や格子点の並びで構成される格子面あるい は、結晶の原子で構成される原子面を表す方法にミラー指数と 呼ばれるものがある。面の方程式に倣って切片を利用する方法 である。面の方程式は、 AxByCz= 1332六方格子のミラー指数 図312六方格子のミラー指数 立方格子との相違→a1,a2,a3,c の4軸を考える点 a1,a2,c 軸をα,β,δで横切る面 a/α :a/β :c/δの最小の整数比h:k:m を求める. 次に最後の指標をl=(hk) のように決める.
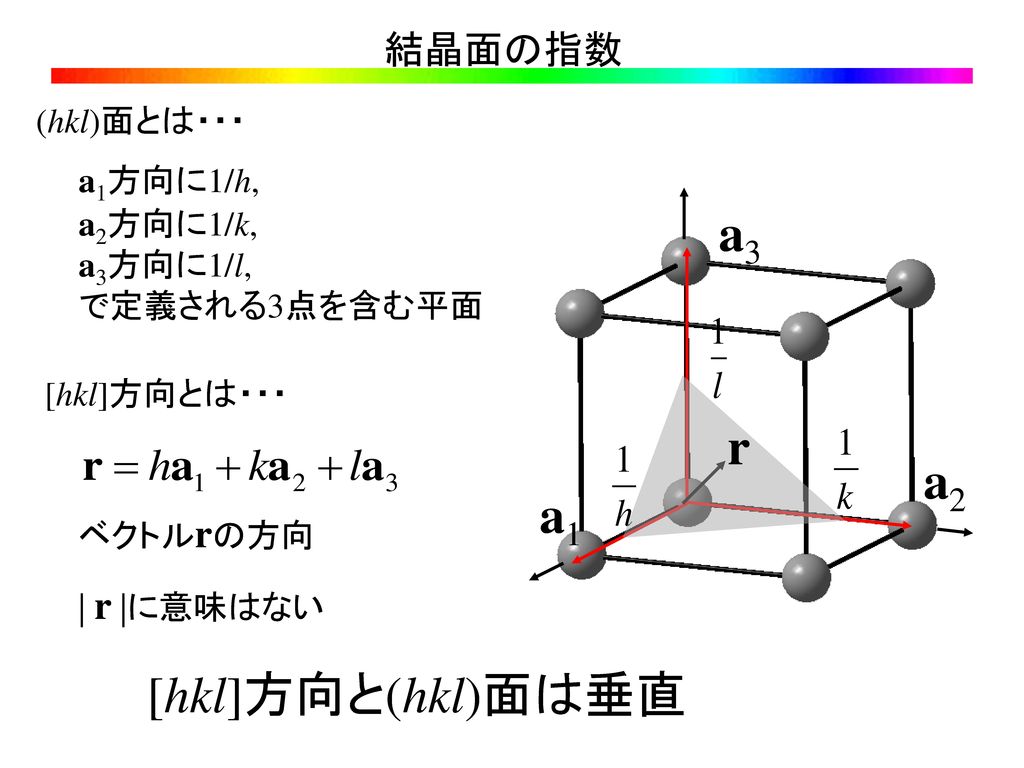
ミラー指数 ミラー指数の表記 < 100>=100,010,001 { 111}=(111),(1 11),(11 1),(111) 方向: 面:19 結晶面の指数 三次元格子の面に対するミラー指数は(h k l)で 与えられる。 1) 格子定数 a 1, a 2, a 3 を単位として面が結晶軸 2 を切り取る長さを表す。 2) これらの数の逆数を求め、じ比を なす3個の最小の整数に簡約する。 これをその結晶面の面指数(h k l)と格子定数 求め方 立方晶 (i) 単位格子一辺の長さ l と原子半径 r の関係 結晶の単位格子の形と大きさを表すパラメーターを「格子定数 (lattice constant) 」といいます。 一般的には、単位格子の各綾の長さ (3 つの結晶軸の各方向にそった繰り返しの周期) の a, b



Space Group For Crystal Structure Analysis




Woa1 化合物エピタキシャル層の製造方法 化合物エピタキシャル層 半導体積層構造および半導体発光デバイス Google Patents
(a)ミラー指数 任意の面の表し方 (1)面と各軸との交点座標(x,y,z)を求める. (2)座標(x,y,z)を各格子定数で割った逆数(h,k,l)を求める. (3)座標成分を最小整数比に直し,括弧にくくって表す. 751 6最密六方格子(hcp)のすべり系 すべり面:{0001}面(等価な面無し) すべり方向:方向(等価な方向が3方向*) すべり系の数:1面×3方向=3個 すべり系の数が少ないため,塑性変形しにくい. *正負を区別しない場合 (区別する場合は×2) 6ミラー指数 463 h2 k2 l2 a:格子定数 面間隔 7 六方晶におけるミラー指数 六方晶における主要な面 結晶方位の表し方



逆 格子 ベクトル 実格子と逆格子の対応 物理のかぎしっぽ



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
Nov 12, · あるすべり面に沿って転位が運動し、ある方向に変位が生じることを、すべり変形という。すべり面とすべり方向の組み合わせをすべり系と呼ぶ。fcc、bcc、hcp金属におけるすべり系を図解する。また活動すべり系を判定するために分解せん断応力を導出し、シュミット因子を用いて考六方晶 六方晶においては慣用的に下図のような a 1 , a 2 , a 3 , c の四つの軸を用いて方向面を表し,指数を( hklm )と書きます。この方法では,Z軸方向の指数は0001となります。この4軸を用いると,a 1 , a 2 , a 3 方向を現す指数 hkl の間には, h k = l立方晶の場合、dとaの関係はミラー指数(hkl)を使って 1 d2 = h2k2l2 a2 (3) となる(課題4)。ちなみに、六方最密充填構造(Hexagonal closepacked)の場合は 1 d2 = 4 3 h2hkk2 a2 ⎛ ⎝⎜ ⎞ ⎠⎟ l2 c2 (4) と表される。それぞれの構造を持つ単位格子の体積を求めた上で、底



Space Group For Crystal Structure Analysis



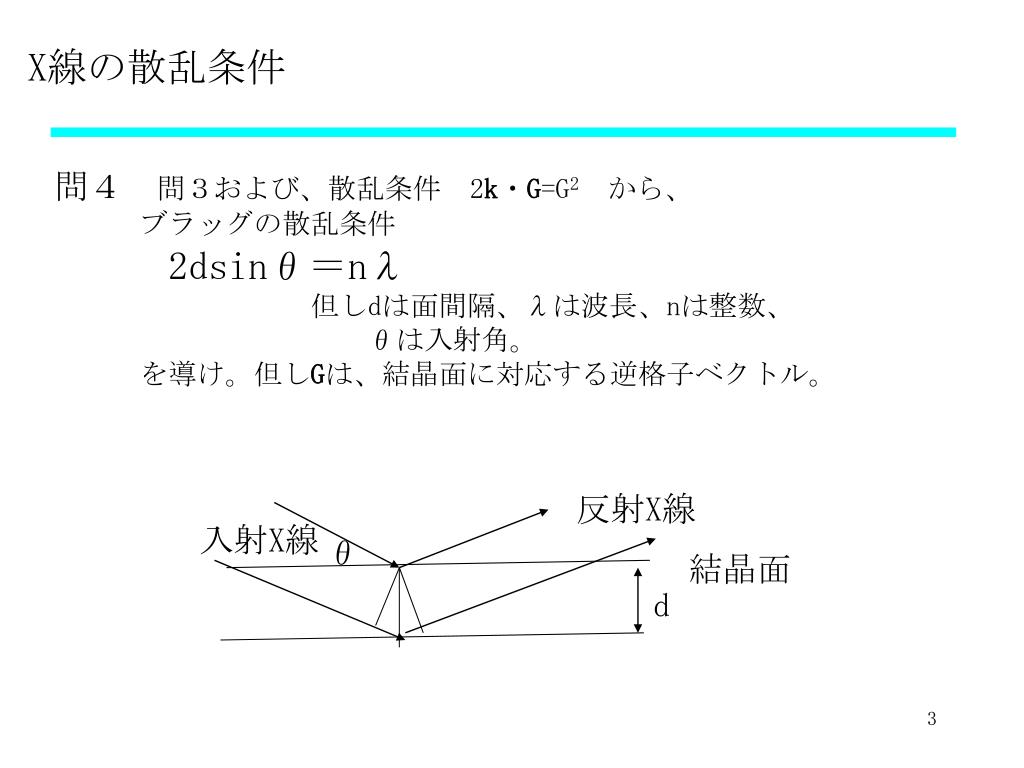
x線結晶解析におけるラウエの条件式とブラッグの条件式
体心立方構造・面心立方構造・六方最密構造 剛球の並べ方と最密構造 剛球を平面上に↓の向きに整列させるのに次の2 つの方法がある。 図より,b の方がa より密であることがわかる。 a b六方最密充填構造(ろっぽうさいみつじゅうてんこうぞう、hexagonal closepacked, hcp)とは、結晶構造の一種である。 学術用語では、稠密六方格子構造(ちゅうみつろっぽうこうしこうぞう)、または単に六方格子構造などと呼ばれる。 六方最密充填構造は一般に正六角柱で表し、この正六角柱の六方晶系の面指数 を用いる (h k l) # (h k j l) A B D O OAB = OAD OBD h k j = 0 利点:面の対称性が明らかになる この2つの面が等価であることがわかる




ミラー指数 Wikiwand



前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download
Aug 07, 12 · 六方晶 ミラー指数 について 今六方晶のミラー指数が 001 100 101 102 110 と表されております。 ここで、この3桁のミラー指数を全て4桁で表すとどのようになりますか?Jul 05, 03 · 六方晶を4つの指数で表現するのは、旧式の方法ですね。関係式は、実際にはhk=lです。 ミラー指数は理解出来ているということなので、ベクトル表現を考えてみてください。ミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。



Images Of 晶系 Japaneseclass Jp



結晶工学特論 第2回目 前回の内容 半導体デバイス Led Ld Hemt 半導体デバイスと化合物半導体 種類の豊富さ 直接遷移型 Ppt Download
座標である). x p =y q z r1 (1) p,q,rは定数のため両側pqrを掛けることができる. qrx p =ry pqz pqr ( )pqr x p( )pqr y q( )pqr z r=pqr 次に,qrをh,prをk,pqをl,pqrをmと置き換える. *1 ミラー自身はヒューウェルの記号をほぼそのまま利用する と明記している(「The Crystallographic Notation adopted in the following Treatise is taken, with a few unimportantまた、六方晶系以外の場合(ほとんど全ての結晶)と六方晶の場合(例外的)で、ミラー指数のつけ方が少々異なる。 六方晶の場合のミラー指数のことを六方晶指数と言うことがある。 目次 1 六方晶系以外の場合 11 方向指数;面心,体 心および六方晶金属の結晶塑性 吉永 日出男* 1緒 言 金属結晶の大部分は面心立方@c),体 心立方(bcc)ま たは稠密六方(hcp)の い・ずれかの結晶構造をもつてい る。化cの中には最も代表的な軽金属であるアルミニウム



x線結晶解析におけるラウエの条件式とブラッグの条件式




Wo11 号 窒化ガリウム系化合物半導体発光素子 Astamuse
Jun 28, 02 · 斜方晶のミラー指数付けと格子定数の求め方 X銭回折で得られたピークの角度からブラッグの式で面間隔を求め、そこから指数付けをしようと思っていますが、どうしてもわかりません。 どうすればいいのか教えてください。 m(__)m ちなみに次の面間隔ここでは、六方晶を例にとってCohenの方法について述べる。六方晶におけるBlagg角 と格子定数およびMiller指数の関係は上に示した通りである。 いま、 λ2 3a2 = A (5) λ2 4c2 = B (6) h2 hk k2 = x (7) l2 = y (8) sin2 θ = z (9) とすれば、 z = Ax+By (10) となる。Aug 25, 18 · つまり、面2のミラー指数だけを考えればよい。 面2を延長させると、y軸の切片はy=1であることがわかる。 それに、z軸の切片がz=1/2であることは、延長させなくても明らかだ。 x軸には平行であるため、最終的なミラー指数は (0,1,2)となる。




Wo10 号 窒化物系半導体素子およびその製造方法 Astamuse




13 0631号 sicエピタキシャルウエハおよびそれを用いたsic半導体素子 Astamuse
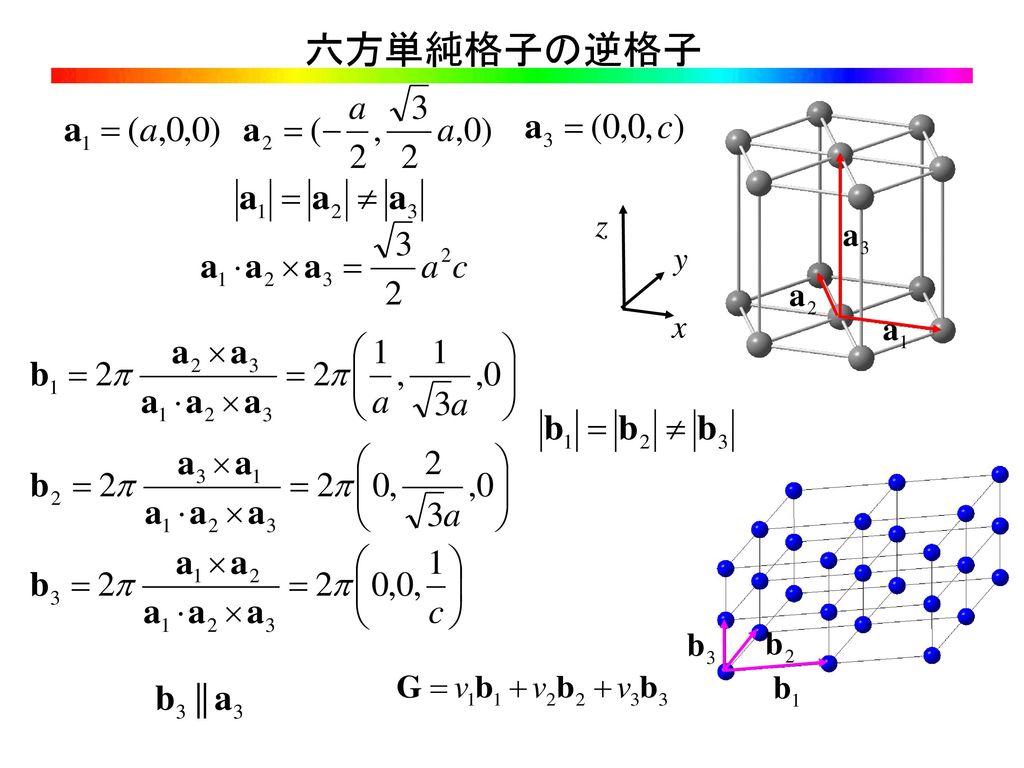
最密六方格子(hexagonal closepacked lattice)の原子配置 軸比(axial ratio) c/aの値.理想的な場合(各原子が球形と見な せる場合)には,軸比が となる.1633= 8/3 単位格子 22図は六方晶を示したものである。 ミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。 六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で問下図のレンガ(辺の長さが異なる直方体)について、属する晶 系、点群、対称要素の種類と場所を示せ。 演習 問a≠b≠c, α≠β≠90º或は1º、γ=90ºなる関係を持つ系は 二斜晶系(diclinic)の定義に一致する。これは8番目の晶系とな るか。 単位胞の選び方



Mukikotaikagaku



逆 格子 ベクトル 実格子と逆格子の対応 物理のかぎしっぽ
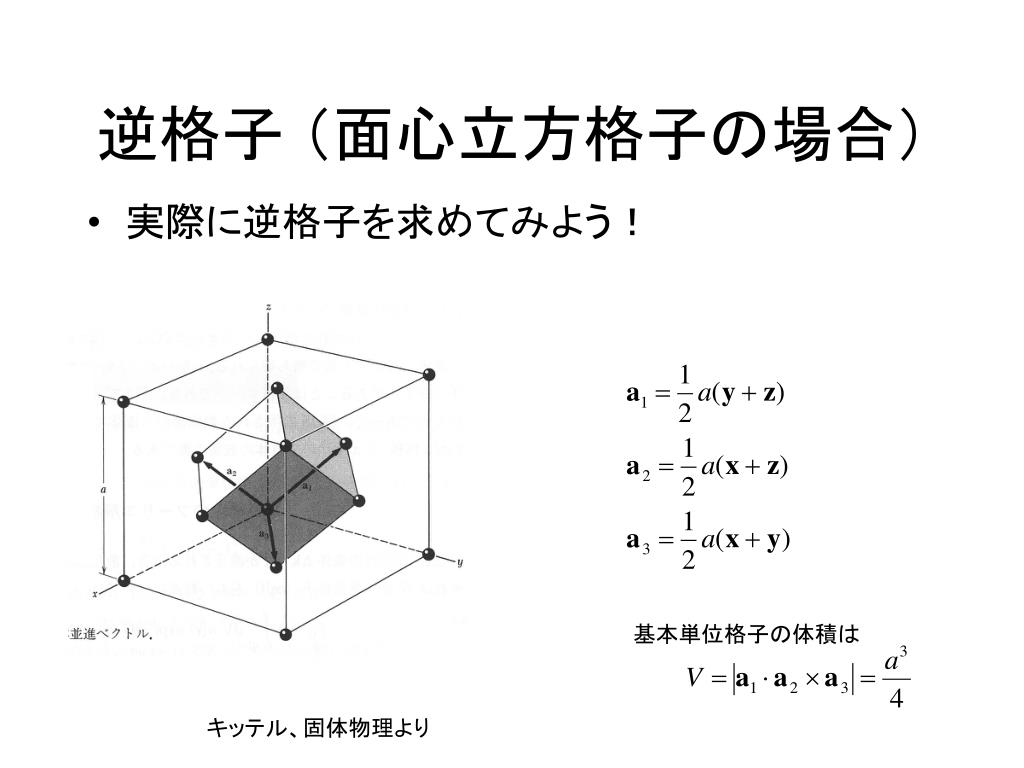
Jun 07, 19 · ミラー指数 ミラー指数の概要 ナビゲーションに移動検索に移動 立方晶結晶での異なるミラー指数をもつ面 方向指数の例 x,y,z軸との切片からミラー指数を決定する例。左は(111)、右は(221)ミラー指数には,面指数と方向指数(方ミラー指数その1:結晶における方向の記述 第7回 ミラー指数その2:六方晶におけるミラー指数 第8回 面間隔の求め方 第9回 格子欠陥(原子空孔と転位)・多結晶体 第10回 x線の発生法・特性x線について 第11回 ブラッグの条件と面六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で 面間隔は 応用 逆格




Wo14 号 半導体発光装置 Astamuse




逆 格子 ベクトル
散乱X 線の強度は式(411) の絶対値の2 乗を計算することで求められる(付録B 参照)。この とき、絶対値が1 となるei(k′·r−!t) の部分はX 線強度の増減に寄与しないから書いても書かなく ても結果は同じミラー指数(ミラーしすう)は結晶の格子中における結晶面や方向を記述するための指数である 。 英国の鉱物学者ウィリアム・ハロウズ・ミラー (William Hallowes Miller) によって考案された。 ミラー指数には、面指数と方向指数(方位指数)の2種類がある。面指数は結晶や格子をどのような平面でFeb 08, 07 · 六方結晶の場合は(0001)というような表し方ですね。 いわゆるc軸が4桁目になります。(h,k,l,m)の場合、h k = l の関係があります。 参考URLに出典例を書きましたが、"ミラー指数" "0001"で検索すると、関連ページが56件ありました。




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download




Woa1 非水電解質二次電池用正極活物質とその製造方法 および 非水電解質二次電池 Google Patents
Dec 26, 19 · 面間隔 指数の隣り合った面間の距離は次の関係で求めることができる。ただし、格子定数を、単位格子の体積をとする。 立方晶: 正方晶: 斜方晶: 六方晶: 単斜晶: 三斜晶: 単位格子の体積 また、単位格子の体積は次の式で求められる。 立方晶: 正方晶: 斜方晶: 六方晶: 単斜晶:




Wo07 号 単結晶サファイア基板 Astamuse




前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download



x線結晶解析におけるラウエの条件式とブラッグの条件式



x線結晶解析におけるラウエの条件式とブラッグの条件式




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度




Woa1 リチウムイオン二次電池用正極活物質及びリチウムイオン二次電池 Google Patents




Woa1 非水電解質二次電池用正極活物質とその製造方法 および 非水電解質二次電池 Google Patents



Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度




13 号 誘電体磁器組成物および電子部品 Astamuse




モデラ Advance Nanolabo ドキュメント



x線結晶解析におけるラウエの条件式とブラッグの条件式




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



結晶とは コトバンク




逆 格子 ベクトル



x線結晶解析におけるラウエの条件式とブラッグの条件式
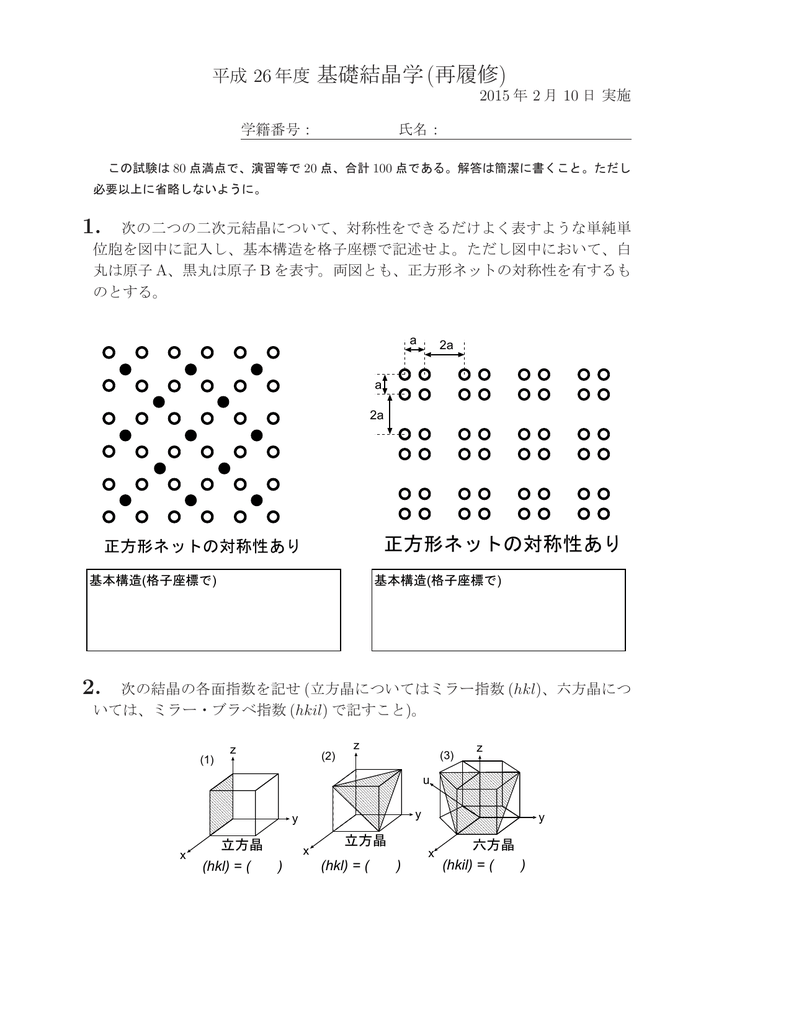



平成 26年度基礎結晶学 再履修




15 号 窒化物半導体構造およびそれを製造する方法 Astamuse




Woa1 リチウムイオン二次電池用正極活物質及びリチウムイオン二次電池 Google Patents




11 号 低濃度アルカリ金属保有の六方晶系ウルツ鉱型エピタキシャル層およびその生成方法 Astamuse




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download



Information




Woa1 リチウムイオン二次電池用正極活物質及びリチウムイオン二次電池 Google Patents




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download




Wo14 号 窒化物半導体発光装置 Astamuse



半導体物理 結晶構造 3 ミラー指数 Sciencompass



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download




ミラー指数 Wikipedia
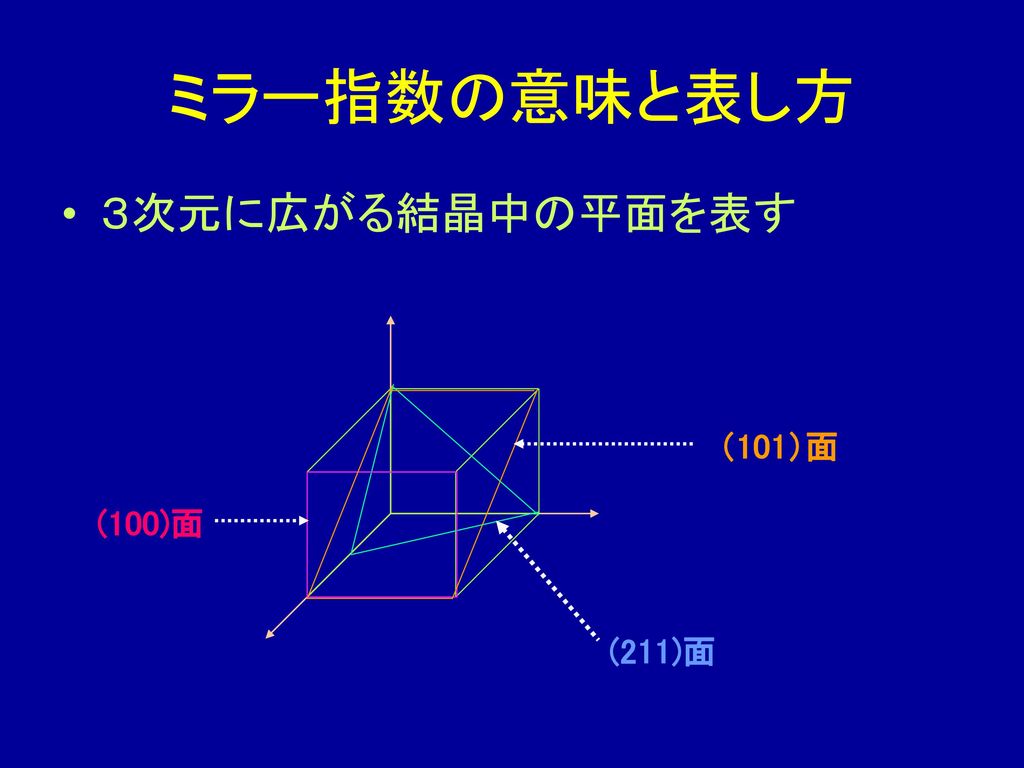



無機化合物の構造と特性 との関係を理解する Ppt Download



Information




2 2 1 ブラベー格子 単位格子 原子が配列している周期的な配列の中で最も 単純で最小な単位 Ppt Download



格子面間隔の計算方法 六方晶 Sciencompass




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download




14 5615号 立方晶炭化珪素半導体基板及び立方晶炭化珪素層 Astamuse




ミラー指数 Monozukuri Hitozukuri 日本のものづくり
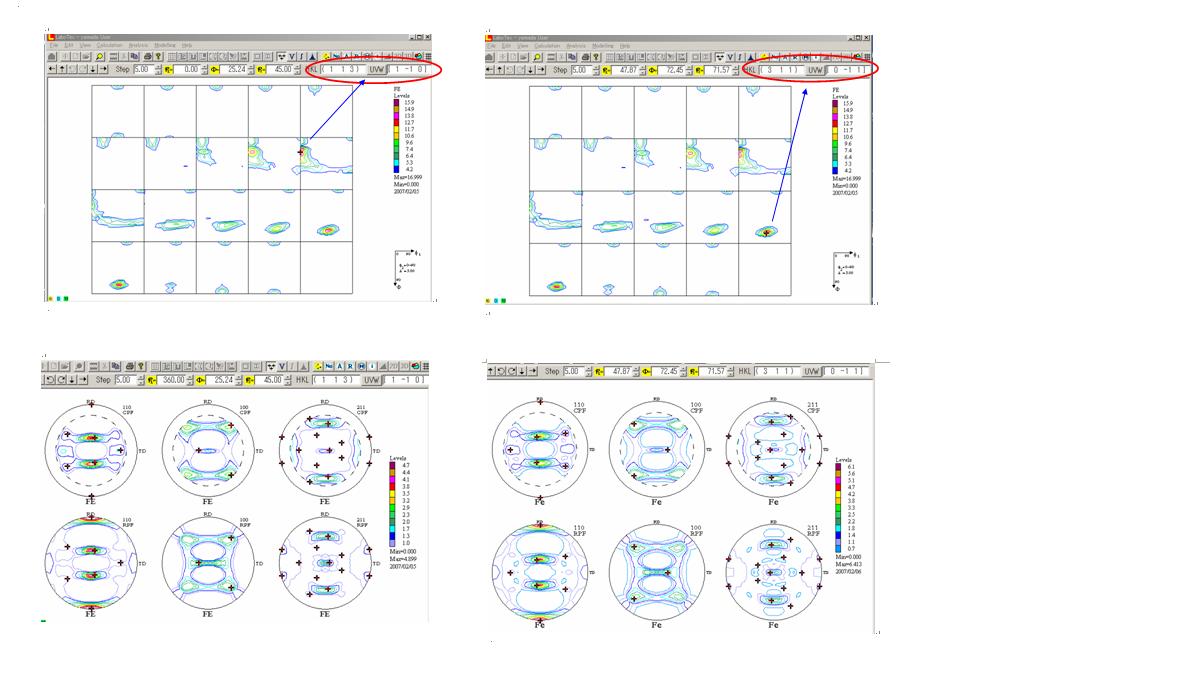



無理やりのfe試料による極点処理 立方晶odf解析シリーズ 方位決定 極点測定 解析 Odf Labotexの導入 helpertex




โน ตของ 専門 講義 結晶構造について ช น Clear



半導体物理 結晶構造について 2 Sciencompass




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



0 件のコメント:
コメントを投稿